Luck, Probability and BlockWithholding Attacks in Crypto Mining

In our last post we worked through Network Difficulty, Share Difficulty and the Hash Function. These are crucial elements in understanding how mining works so would definitely recommend reading through that post before diving into mining luck.

In this post we talk about what Luck is, how it is calculated, how it can be analyzed and what it means for different industry players.

Simplified Definition

The Luck of crypto mining is probabilistic in nature. Imagine that each miner is given a lottery ticket for a certain amount of hashing power they provide. For illustrative purposes imagine that you provide 1 EH/s of hashing power and the overall hashing power in the network was 100 EH/s then you would receive 1 of 100 total lottery tickets. The probability of you winning the lottery (finding the block reward) would be 1%. So for every 100 blocks found you should statistically find 1 of them.

Now imagine that you found 2 out of the 100 blocks, this means that you found a block earlier than you statistically should. You are lucky! Now imagine you found 0 out of 100. This would make you unlucky. Over the long run, statistically you should find on average 1 out of 100 (1%) blocks, but there is short term variance.

The above description should give you a base level understanding of Luck, but if you want to dive into it deeper keep following below!

Key Terms

Mining Pool

A Mining Pool is a group of miners that work together to reduce the volatility of their returns. Miners share their processing power over a network, and then split the reward according to the amount of work they contributed to finding the block, and a fee is given to the pool operator.

Mining in pools began when the difficulty for mining increased to the point where it could take years for smaller miners to find a block by themselves (hence earn a payout for their efforts). The solution to this problem was for miners to pool their resources so they could generate blocks more quickly and therefore receive a portion of the block reward on a consistent basis.

Pay-Per-Share

Pay-Per-Share (“PPS”) is a payment system employed by some Mining Pools. The miner gets paid on what is statistically probable rather than what actually occurs. What this system ultimately does is take out the “luck” and hence variance in a miner’s payout. Instead the pool operator absorbs all the risk of variance.

PPLNS

PPLNS is another popular payment method, which offers payment to miners as a % of shares they contribute to the total shares. Miners only get paid out once a block is actually found (not if it is only statistically probable).

For more details on PPS vs PPLNS you can check out this article.

Calculating Luck

Probability of Mining a Block

The probability of mining a block is 1/(²³²\*Difficulty) for each hash.

As of Feb-19–2020 the Bitcoin Difficulty is 15,546,745,765,549.

So the chances of mining a block with a single hash is 0.000000000000000000001498%.

Luck

The correct way to calculate luck is to look at the amount of expected shares per round and the actual amount submitted.

Luck = mean(expected shares per round / actual shares per round)The larger the Luck, the better the mining ‘luck’. A Luck of 200% means you submitted half as many shares as you should have to find a block.

Luck Statistic

The Luck Statistic is the inverse of the above. This is how we look at it as a Mining Pool operator.

Luck Statistic = mean(actual shares per round / expected shares per round)The smaller the Luck Statistic, the better the ‘luck’. A Luck Statistic of 0.5 means you submitted half as many shares as you should have to find a block.

Variance in Luck

When looking at Luck over a period, it should never be done in time (hours, days etc), rather it should be as a number of blocks.

This is especially important when drawing conclusions on Luck or comparing two different miners. One miner may have mined more blocks than the other, which significantly impacts the way we think about Luck.

Visualizing the Luck Statistic

Finding the Proper Distribution

Starting with the basic Poisson Distribution, it is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event. The problem with the Poisson Distribution is that it is discrete and not continuous. The Poisson Distribution deals with the number of occurrences *in a fixed period of time. *This is not the way we want to look at the Luck Statistic.

The next step is to check the Gamma Distribution, which is continuous. The Gamma Distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average rate. The gamma distribution, predicts the time until the k-th event occurs. When the shape parameter of the Gamma Distribution has an integer value, the distribution is called the Erlang Distribution. This is important for looking at the Luck Statistic because it will always be a positive integer.

The Luck Statistic is negative binomially distributed, so can be approximated using the Erlang Distribution.

Erlang Distribution

We don’t need to go deep into the formula of this distribution, but the Erlang Distribution can be thought of as a generalization of the exponential distribution, a continuous distribution that is commonly used to measure the expected time for an event to occur (i.e. mine a block).

Using this distribution makes calculating luck much simpler and it actually becomes more accurate as the Network Difficulty increases. At the current Network Difficulty it shouldn’t result in more than a millionth of a % in error.

If that was hard to follow the next section should help you visualize it.

Probability Density Function (PDF)

Using the Erlang Distribution, the PDF indicates how probable it is that the Luck Statistic will be some arbitrary value. At any time the probability of the Luck Statistic being an exact number (i.e. 1.00000000000) is 0%. Rather the PDF can be used to specify the probability of the Luck Statistic falling within a particular range of values (i.e. below 1.0).

For reference the formula can be found below.

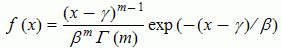
You can use R or python to calculate the PDF yourself. But a simpler way to do it is to use the Wolfram Alpha website.

For DIY calculations: quantile(ErlangDistribution[Number of Blocks, Number of Blocks], optional %)

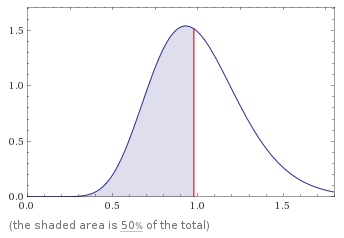
Plotting out the PDF for 1 Block shows us a high range of potential outcomes. This means that there is a high likelihood of a Luck Statistic far away from the mean of 1.0.

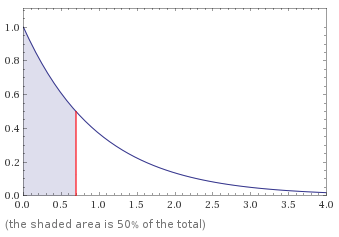
If we increase the amount of blocks to 14, which is roughly 10% of the daily network reward then we can see the distribution starting to become more normalized. There is now a higher likelihood that the the Luck Statistic will be closer to 1.0 but there is still a lot of room for variability.

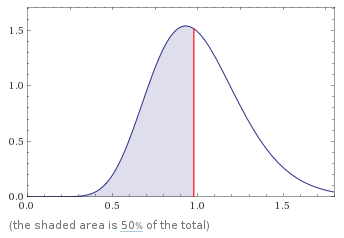
If we increase the amount of blocks to 144, which is 100% of the daily network reward then we see a normal curve with a fairly tight range of potential outcomes. It would be very unlikely for luck to be below 0.7 or above 1.3 averaged over the 144 blocks.

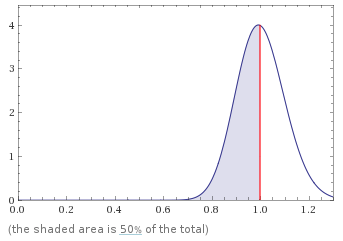
The PDF is useful in understanding the importance of looking at the Luck Statistic on a large sample (i.e. averaged over more blocks).

Cumulative Distribution Function (CDF)

The CDF is a great way to analyze your Luck Statistic. Let’s say your mining pool had a Luck Statistic of 1.3 over the past 1, 10 and 140 blocks. Is that just unlucky or is that nearly impossible (and raises other questions).

Again, you can use R or python to model this out but can also use the Wolfram Alpha website or excel.

Wolfram Alpha: CDF[ErlangDistribution[nblocks, nblocks], Luck Statistic]

Excel: =GAMMA.DIST(Luck Statistic, nblocks, 1 / nblocks, 1)

The result of a 1.3 Luck Statistic for 1 block will show 0.727468. This means that ~73 times out of one hundred re-runs of one block, we’d see luckier blocks. Or 73% of the time it would be luckier. That is not very unlucky. 27% of the time there would be an unluckier block.

We put together this table to show the probability of having a specific Luck Statistic for a number of blocks. As you can see there are times where the Luck Statistic is too bad to be probable (i.e. a 1.5 Luck Statistic averaged over 60 blocks).

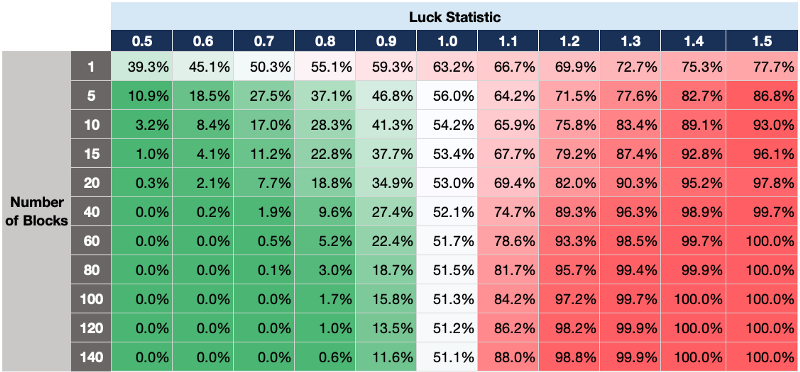
We don’t often care about the other side too much, because we aren’t losing money, but it could be a reason to check to make sure your data is correct (i.e. a 0.5 Luck Statistic averaged over 60 blocks).

Outcome

PPS Pool

As we described in the beginning, a PPS pool takes the variance out of mining for it’s miners. So bad luck hurts the pool, good luck helps the pool and their miners are never impacted. The only time it is a concern for their miners is if a pool goes bankrupt and their outstanding balance is lost + some downtime until they switch to a new pool.

As a PPS pool operator, we track our luck very carefully. We want to make sure that we have enough liquidity to cover short term variance. We also want to make sure that everything is operating correctly. This comes up mostly during times of bad luck, we check to make sure it is possible that we are indeed that unlucky. If we see that we have worse luck than 99% of the time than we start considering other factors such as attacks on our pool or technical bugs. We will talk through an example of a pool attack below.

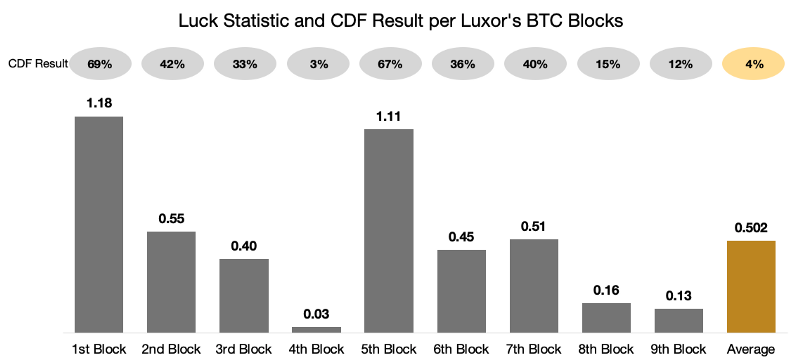
Since we launched our Bitcoin Pool we have found 9 blocks, for an average luck of 0.502. As a Pool Operator we are happy about this, but it is still in the realm of possibility (4% of the time it would be better). We know from running our other 10 pools that periods of bad luck are just as likely, so we do not expect this to continue.

PPLNS Pool

PPLNS pools operate opposite to PPS. Instead of the pool bearing the variance risk it is now put on the miners. Periods of bad luck mean that miners get less reward, but periods of good luck means they get more.

For PPLNS pools, miners are likely to leave after a period of bad luck. An issue with this is known as Gambler’s Fallacy, which is the belief that if a particular event occurs more frequently than normal during the past it is less likely to happen in the future (or vice versa). The next pool may not have any better luck.

Miners on a PPLNS pool should monitor their pool’s luck closely. If the bad luck seems impossibly bad then the pool could be getting attacked or has a bug.

BlockWithholding Attack

This is one of the most common attacks on Mining Pools and usually comes from other competitor pools looking to (A) bankrupt them if they are a PPS pool or (B) have their miners leave them if the are a PPLNS pool.

BlockWithholding occurs when a miner does not return the valid hashes that they create.

The attacker (miner) would set some custom specification not to return a hash that is smaller than a preset size. That preset size is usually slightly below the Network Target (inverse of difficulty). So the miner would still be getting paid for the shares they submit to the pool that are above the Share Target but below the Network Target. The miner would never send the pool a hash that is a valid block. Because the miner is paid as if they could produce a network block, a PPS pool loses money and a PPLNS pool’s miners lose revenue.

There are ways that pools try to defend against these attacks but there is no clear, foolproof way. It is usually done by pools monitoring the individual luck of their miners and locking their account after it becomes impossible that they haven’t produced a hash below the Network Target.